Analýza časových radov
Definícia časového radu
Časový rad predstavujú dáta, ktoré sledujú vývoj danej veličiny v čase, pričom všetky hodnoty sú merané v rovnakej jednotke a s rovnakou periodicitou sledovania. Ak je perióda sledovania kratšia ako jeden rok, hovoríme o krátkodobom časovom rade, inak hovoríme o dlhodobom časovom rade.
Časový rad môžeme zapísať v tvare yt = Dt + St + εt, kde Dt vyjadruje jeho deterministickú zložku, St jeho sezónnu zložku a εt je chybová, poruchová alebo náhodná zložka.
Zhrnutie: Časového radu
- Časový rad je súbor údajov meraných v čase s rovnakou periodicitou a jednotkou.
- Krátkodobý časový rad: perióda < 1 rok
- Dlhodobý časový rad: perióda ≥ 1 rok
- Zápis: yt = Dt + St + εt
- Dt – deterministická (trendová) zložka
- St – sezónna zložka
- εt – chybová alebo náhodná zložka
Základné štatistiky
Na zistenie základných štatistík (minimum, maximum, medián, priemer) časového radu nám poslúži funkcia:
summary(premenna)
Min. 1st Qu. Median Mean 3rd Qu. Max.
192.6 231.2 351.8 331.4 404.6 494.3
Identifikácia sezónnosti
Prvým krokom pri identifikácii sezónnosti ľubovoľného časového radu je takmer vždy zobrazenie jeho grafu. Z neho je možné určiť základné charakteristické vlastnosti skúmaného radu, medzi ktoré patrí tiež prítomnosť či neprítomnosť sezónnej zložky.
Sezónne dáta – načítanie dát
yt = scan()
Dáta môžete nájsť TU.
Pomocou funkcie ts vytvoríme časový rad objektov. Úprava vstupných dát týmto spôsobom je nevyhnutná pre ďalšiu prácu s funkciou stl,
o ktorej bude reč neskôr, a taktiež je potrebná pre mnohé ďalšie funkcie v prostredí R, ktoré pracujú s časovými radmi.
yt <- ts(yt, start=1956, freq=12)
# dáta sú mesačné (freq=12) a začínajú rokom 1956
Ak by dáta začínali napríklad júnom 1956, príkaz bude nasledovný:
ts(yt, start=c(1956,6), frequency=12)
Pomocou funkcie plot vykreslíme graf, na základe ktorého môžeme predbežne zistiť, či časový rad obsahuje sezónnu zložku:
plot(yt, type="l")
# pomocou parametru type="l" použijeme čiarový graf
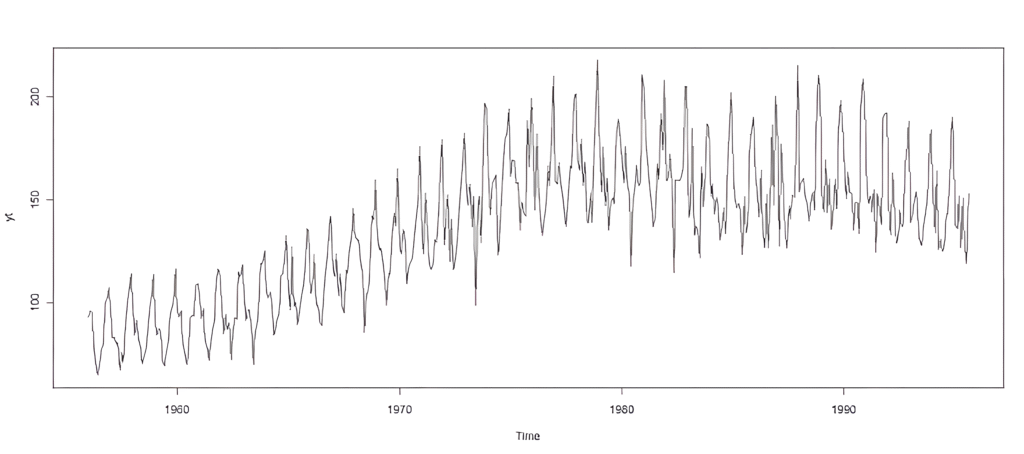
Zistenie sezónnosti
Zistenie prítomnosti sezónnosti, alebo dokonca jej identifikácia (t.j. určenie periódy), môžeme jednoducho vykonať pohľadom na graf priebehu časového radu. Často je totiž sezónnosť tak zrejmá, že nie je potrebné ďalšie testovanie.
Ako ďalšia pomôcka pri zobrazovaní sezónnosti nám môže pomôcť funkcia seasonplot z knižnice forecast.
Nasledovným príkazom zobrazíme sezónny graf, pričom dáta “rozkúskujeme” po roku a zobrazia sa nám všetky hodnoty v rozmedzí jedného roka.
Môžeme tiež pridať parameter year.label=TRUE, ktorý zobrazí roky pri dátach (v tomto prípade nebol použitý kvôli ich množstvu).
Farebnosť grafu môžeme upraviť cez parameter col alebo úplne odstrániť.
Menením hodnôt vo funkcii rainbow() môžeme zmeniť farby kriviek.
seasonplot(yt, col=rainbow(40), type="b", xlab="Mesiac")
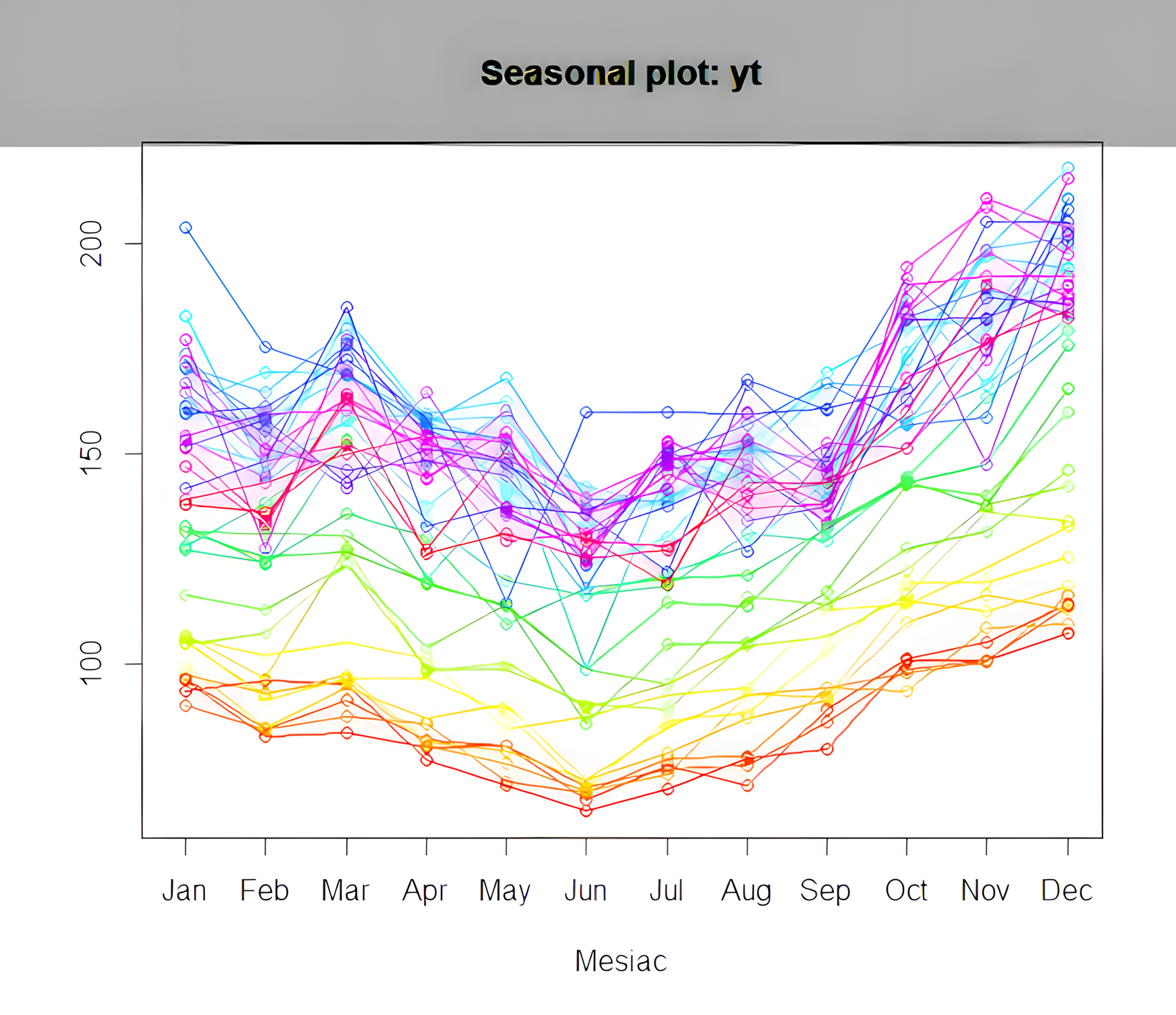
ACF a PACF – identifikácia modelu
Vo všeobecnosti je však možné použiť metódy, ktoré nám potvrdia prítomnosť sezónnej zložky. Pri skúmaní sezónnych výkyvov časového radu je vhodné zobraziť priebeh jeho autokorelačnej funkcie (ACF) alebo parciálnej autokorelačnej funkcie (PACF).
Tieto funkcie sú významným nástrojom najmä pri identifikácii ARIMA procesov, no slúžia aj na skúmanie prítomnosti sezónnej zložky v časových radoch. Ak sa vysoká hodnota koeficientu autokorelácie opakuje každých k posunov, je možné predpokladať, že ide o dôsledok sezónnosti.
Príklad na ACF a PACF v ARIMA modeloch
| ACF | PACF | Model |
|---|---|---|
| Pozvoľne utlmovaná | Náhle utlmená po posune p | AR(p) |
| Náhle utlmená po posune q | Pozvoľne utlmovaná | MA(q) |
| Pozvoľne utlmovaná | Pozvoľne utlmovaná | ARMA(p,q) |
Periodogram a STL rozklad
Pri odhaľovaní sezónnej zložky nám môže byť taktiež veľmi nápomocný periodogram. Používa sa na detekciu a prípadnú kvantifikáciu periodických zložiek v časových radoch.
spec.pgram(yt, log="no", taper=0)
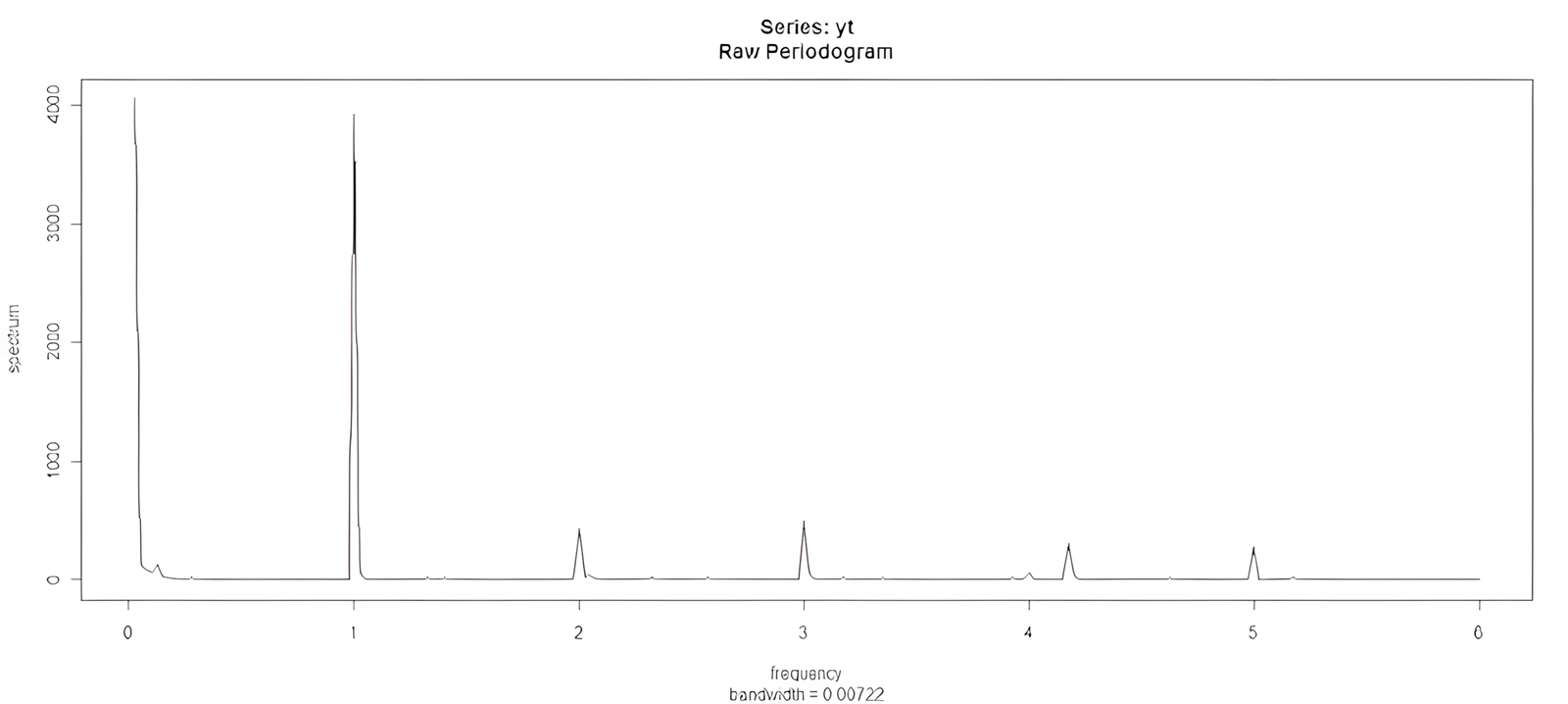
V R existuje veľmi pekná funkcia stl, ktorá rozloží časový rad na trendovú, sezónnu a náhodnú zložku.
plot(stl(log(yt), s.window="periodic"))
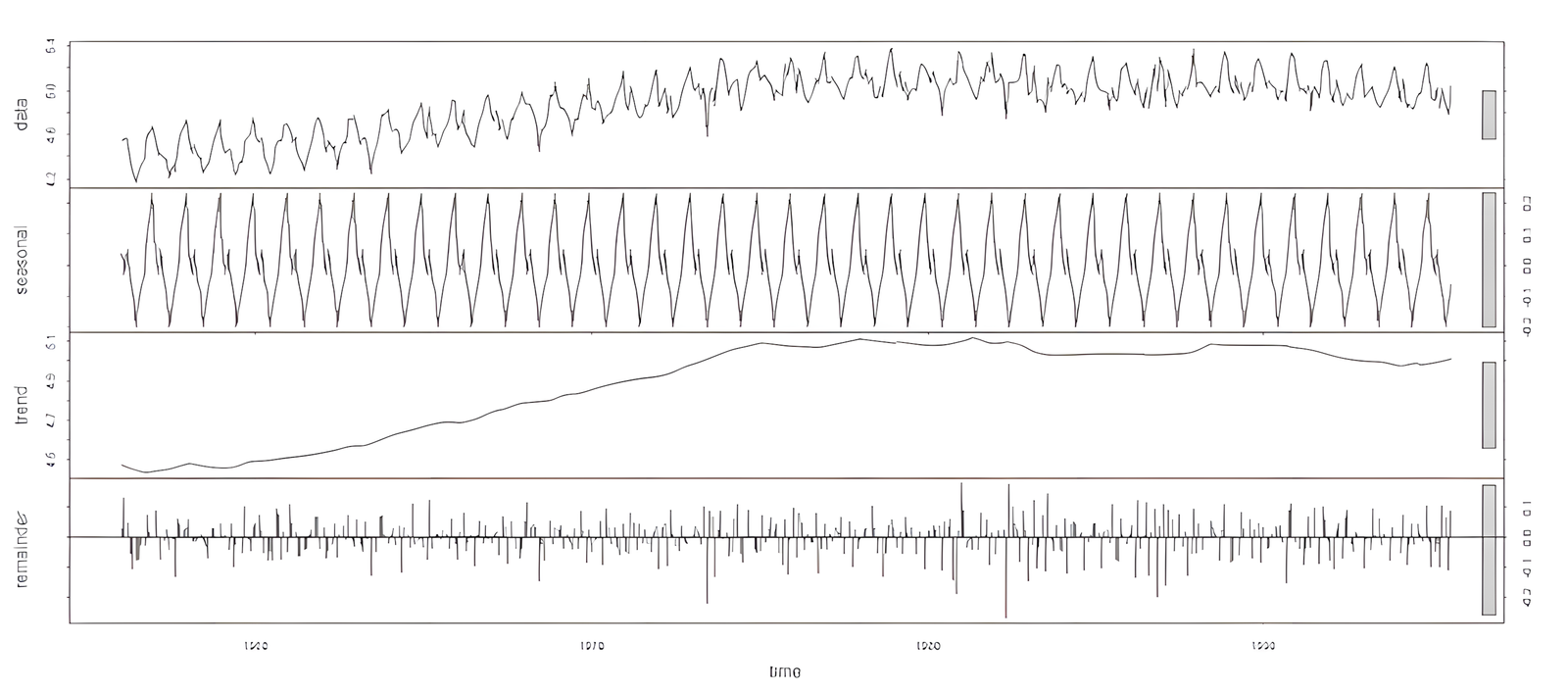
Jurčo, M.: DIPLOMOVÁ PRÁCA: Modelovanie sezónnosti v ekonomických procesoch s využitím aplikácie Open source. 2010
Polívka, L.: DIPLOMOVÁ PRÁCA: Moderné prognostické metódy v modelovaní podnikových procesov. 2010
Falát, L., Laštík, T., Tkáč, P.: FRI MANUÁL v1.0
Kauzálne prognostické modely [4.6. 2015]
Vyrovnávanie časových rádov [4.6. 2015]
