ARIMA modely v R
ARIMA modely (Autoregressive Integrated Moving Average) patria medzi základné nástroje pre modelovanie časových radov. Zachytávajú závislosti medzi predchádzajúcimi hodnotami a náhodnými zložkami série.
Potrebné knižnice:
tseries– preKPSStest stacionarity
Čoskoro bude text rozšírený.
Identifikácia modelu
Prvým krokom k správnemu modelovaniu ekonomických procesov a prognózovaniu je správna identifikácia modelu. Používajú sa pri tom:
- Autokorelačné (ACF) a
- Parciálne autokorelačné (PACF) koeficienty,
ktoré vizualizujeme pomocou tzv. korelogramov.
ACF a PACF v R
Funkcia acf() je v R dostupná štandardne. Môžeme ju použiť nasledovne:
acf(x, lag.max = NULL,
type = c("correlation", "covariance", "partial"),
plot = TRUE, na.action = na.fail, demean = TRUE, ...)
Jednoduchý výpočet a uloženie výstupu:
acf1 = acf(yt)
Vypísanie koeficientov uložených v premennej acf1:
acf1
Príklad výstupu (Autocorrelations of series ‚yt‘ by lag):
Lag: 0 1 2 3 4 5 6 7 8 9 10
1.000 0.494 -0.050 -0.265 -0.283 -0.072 0.219 0.196 -0.012 -0.093 -0.106
11 12 13 14 15 16 17 18 19 20
-0.075 0.031 0.014 -0.105 -0.124 -0.112 -0.091 0.003 0.157 0.182
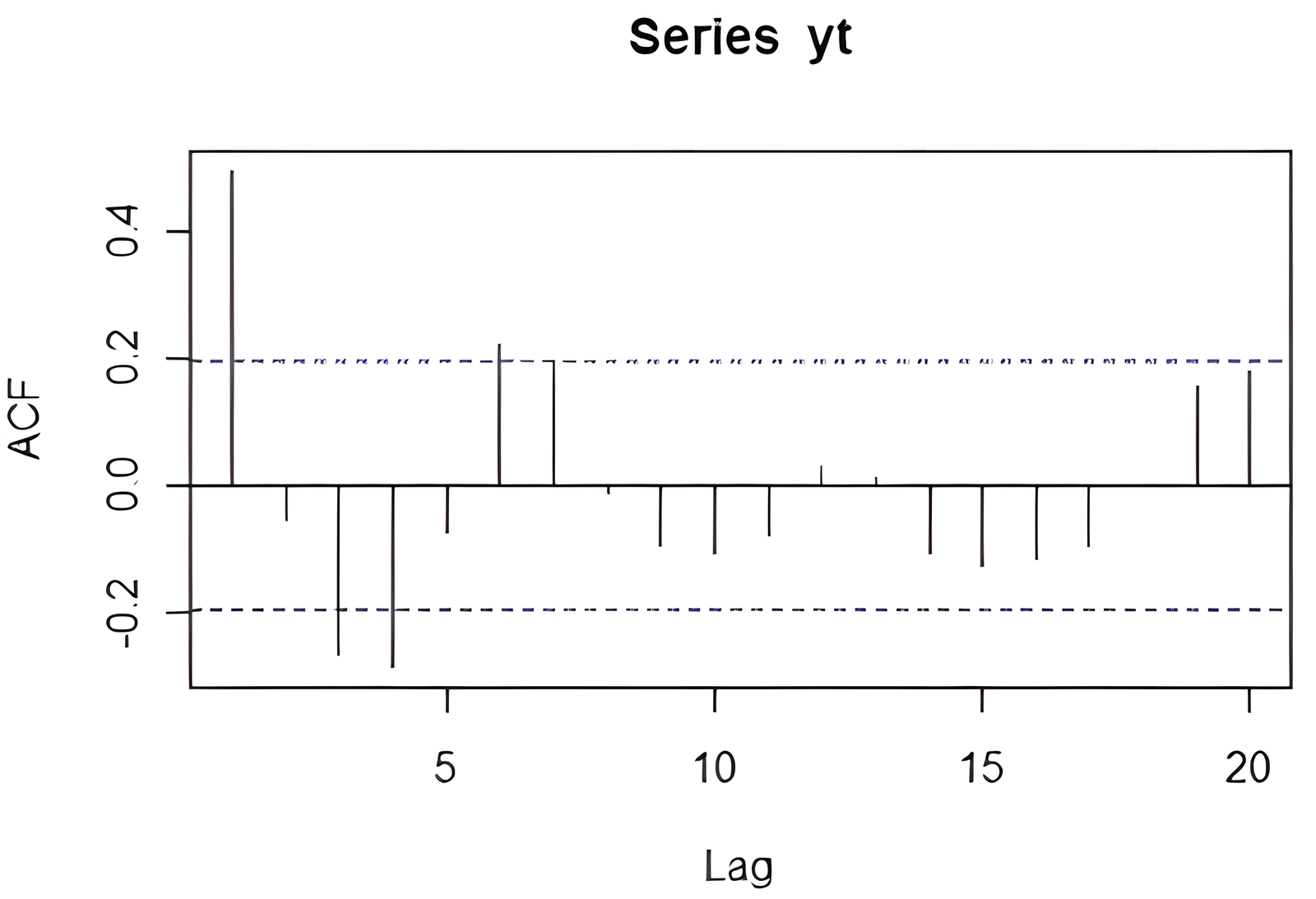
Na vykreslenie korelogramu použijeme:
plot(acf1[1:100])
Poznámka: Hodnota pri posune 0 (lag = 0) je vždy 1 a nemá pre analýzu význam, preto sa často vizualizuje až od posunu 1.
Dáta použité v tomto príklade nájdete v časti Odkazy na použité a reálne dáta.
PACF funkcia v R
Podobne ako pri ACF, aj PACF (parciálna autokorelácia) umožňuje identifikovať vhodný AR (autoregresný) člen modelu. Slúži na určenie priameho vplyvu konkrétnych predchádzajúcich hodnôt bez sprostredkovania cez iné.
V R môžeme funkciu použiť nasledovne:
pacf(x, lag.max = NULL, plot = TRUE, na.action = na.fail, ...)
Príklad výpočtu a uloženia výstupu do premennej:
pacf1 = pacf(yt)
Vypísanie koeficientov parciálnej autokorelácie:
Partial autocorrelations of series ‘yt’, by lag
Lag: 1 2 3 4 5 6 7 8 9 10 11
0.494 -0.388 -0.060 -0.149 0.133 0.163 -0.127 -0.062 0.065 -0.018 -0.034
12 13 14 15 16 17 18 19 20
-0.004 -0.104 -0.072 -0.022 -0.100 -0.052 -0.005 0.164 0.053
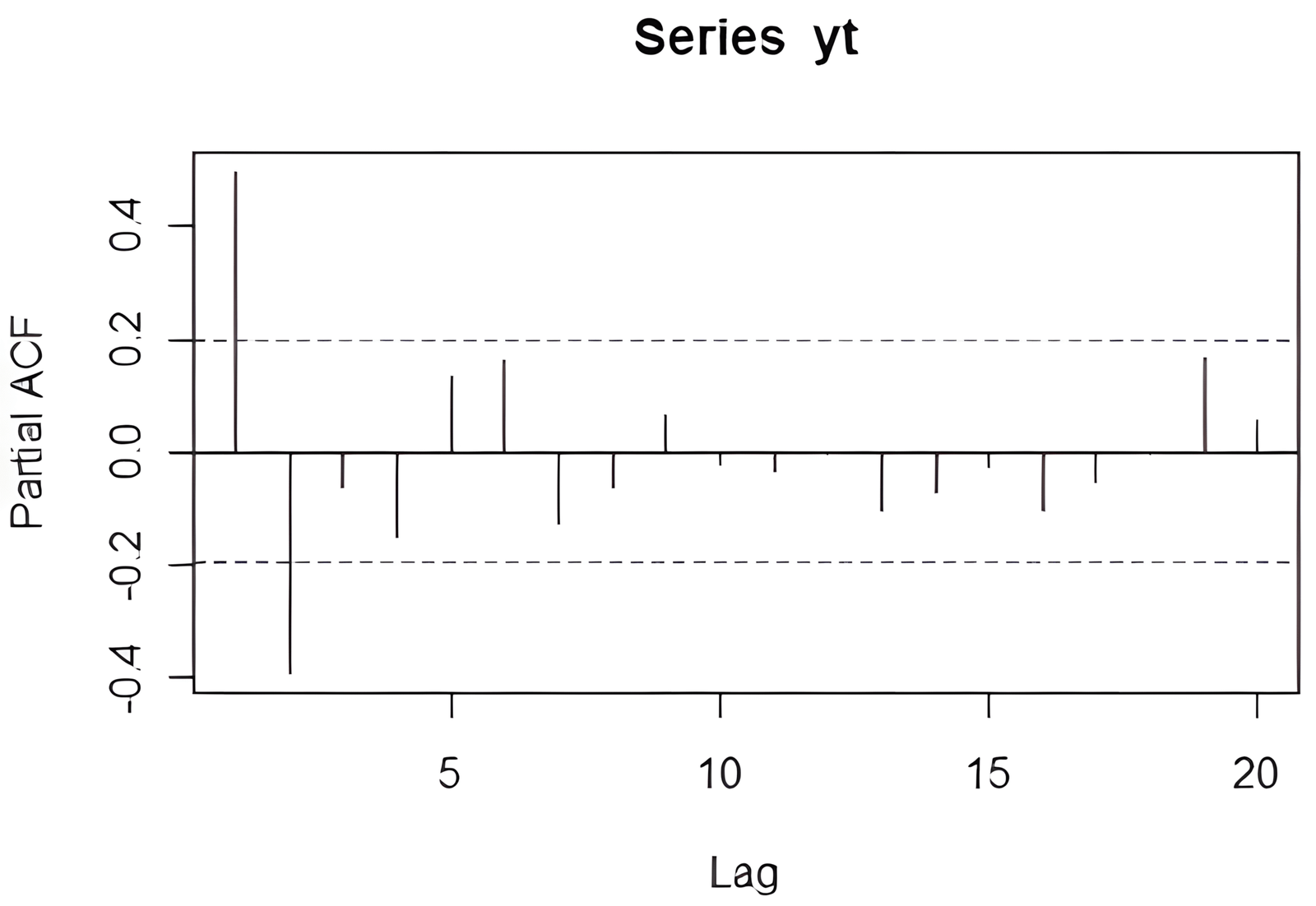
Vizualizácia parciálneho korelogramu:
plot(pacf1[1:100])
Poznámka: Keďže pacf() nezačína od lag 0, nemusíme odstraňovať prvý posun ako pri ACF. Výsledný korelogram vizualizuje priamy vplyv jednotlivých časových posunov.
Identifikácia ARIMA modelu a stacionarita časového radu
Identifikácia správneho ARIMA modelu sa často začína analýzou ACF a PACF. Podľa ich priebehov môžeme odhadnúť, či ide o model typu AR(p), MA(q) alebo ARMA(p, q).
Príklad: Na základe správania PACF (dva výrazné koeficienty) môžeme identifikovať model AR(2).
Nie vždy je identifikácia jednoznačná, preto môžeme použiť AIC kritérium (Akaike Information Criterion). Nižšia hodnota AIC znamená lepší model. V R sa počíta automaticky pri odhade parametrov modelu.
Stacionarita časového radu
Stacionarita je nevyhnutná podmienka pre použitie ARMA modelov. Overuje sa viacerými spôsobmi:
- Analýza tvaru ACF (dlhé pomalé klesanie často značí nestacionaritu)
- KPSS test na úroveň stacionarity
kpss.test(yt)
Výsledok: Ak je p-value > hladina významnosti, stacionarita sa nepotvrdzuje – rad je stacionárny.
Úprava nestacionárneho radu
Ak časový rad nie je stacionárny, môžeme ho transformovať pomocou:
- Odstránenia trendu:
detrend(yt) - Logaritmovania:
log(yt) - Diferencovania:
diff(yt) - alebo ich kombináciou (napr. logovanie + diferenciácia)
Po úprave je vhodné znova overiť stacionaritu.
Odhad parametrov ARIMA modelu
Po identifikácii a stacionarizácii časového radu nasleduje odhad parametrov modelu. V R na to slúži funkcia arima(), ktorá má viacero parametrov, no najdôležitejšie sú:
x– časový rad (napr.yt)order = c(p, d, q)– kdepje stupeň AR,dstupeň diferencie,qstupeň MA
Príklad odhadu modelu AR(2):
ar2 = arima(yt, order = c(2, 0, 0)) ar2
Výstup:
arima(x = yt, order = c(2, 0, 0))
Coefficients:
ar1 ar2 intercept
0.7108 -0.4249 28.6500
s.e. 0.0923 0.0936 0.4559
sigma^2 estimated as 10.55: log likelihood = -260.02, aic = 528.04
Získanie konkrétnych parametrov modelu:
ar2$coef # Výstup: # ar1 ar2 intercept # 0.7108021 -0.4248993 28.6500239
Porovnanie modelov pomocou AIC
Hodnota AIC (Akaike Information Criterion) slúži na porovnanie modelov – nižšia hodnota značí lepší model.
Vyskúšame alternatívny model ARMA(2,1):
ar3 = arima(yt, order = c(2, 0, 1)) ar3
Coefficients:
ar1 ar2 ma1 intercept
0.8676 -0.4997 -0.1922 28.6525
s.e. 0.2067 0.1187 0.2388 0.4161
sigma^2 estimated as 10.49: log likelihood = -259.79, aic = 529.57
Keďže hodnota AIC = 529.57 je vyššia ako pri predchádzajúcom modeli (528.04), pôvodný model AR(2) je lepší.
Kontrola reziduí modelu (ARCH test)
Po odhade parametrov modelu je dôležité overiť kvalitu reziduí. Jedným z nástrojov je ARCH test, ktorý zisťuje prítomnosť podmienenej heteroskedasticity v reziduách.
ARCH test je súčasťou balíka FinTS, ktorý je potrebné nainštalovať:
install.packages("FinTS")
library(FinTS)
Štruktúra testu:
ArchTest(x, lags = 12, demean = FALSE) # kde: # x - vektor reziduí # lags - počet posunov (typicky 1, 5, 12)
Získanie reziduí z ARIMA modelu a aplikácia testu:
ArchTest(ar2$residuals, lags = 1)
Výstup testu:
ARCH LM-test; Null hypothesis: no ARCH effects data: ar2$residuals Chi-squared = 0.0573, df = 1, p-value = 0.8109
Keďže p-value = 0.8109 je väčšie ako typická hladina významnosti (napr. 0.05), reziduá neobsahujú ARCH efekt a teda model je z pohľadu reziduí v poriadku.
Predikcia časového radu (ARIMA)
Na prognózovanie hodnôt časového radu sa využíva funkcia predict(). Vstupnými parametrami sú odhadnutý ARIMA model a počet požadovaných predikovaných hodnôt.
prog = predict(ar2, 9)
Výstup z funkcie:
$pred – Predikované hodnoty:
Time Series: Start = 101 End = 109 Frequency = 1 [1] 32.15551 29.53138 27.78701 27.66211 28.31450 28.83130 28.92144 28.76592 28.61708
$se – Štandardné chyby predikcie:
[1] 3.247405 3.984184 3.992717 4.071160 4.126931 4.129397 4.133579 4.138070 4.138477
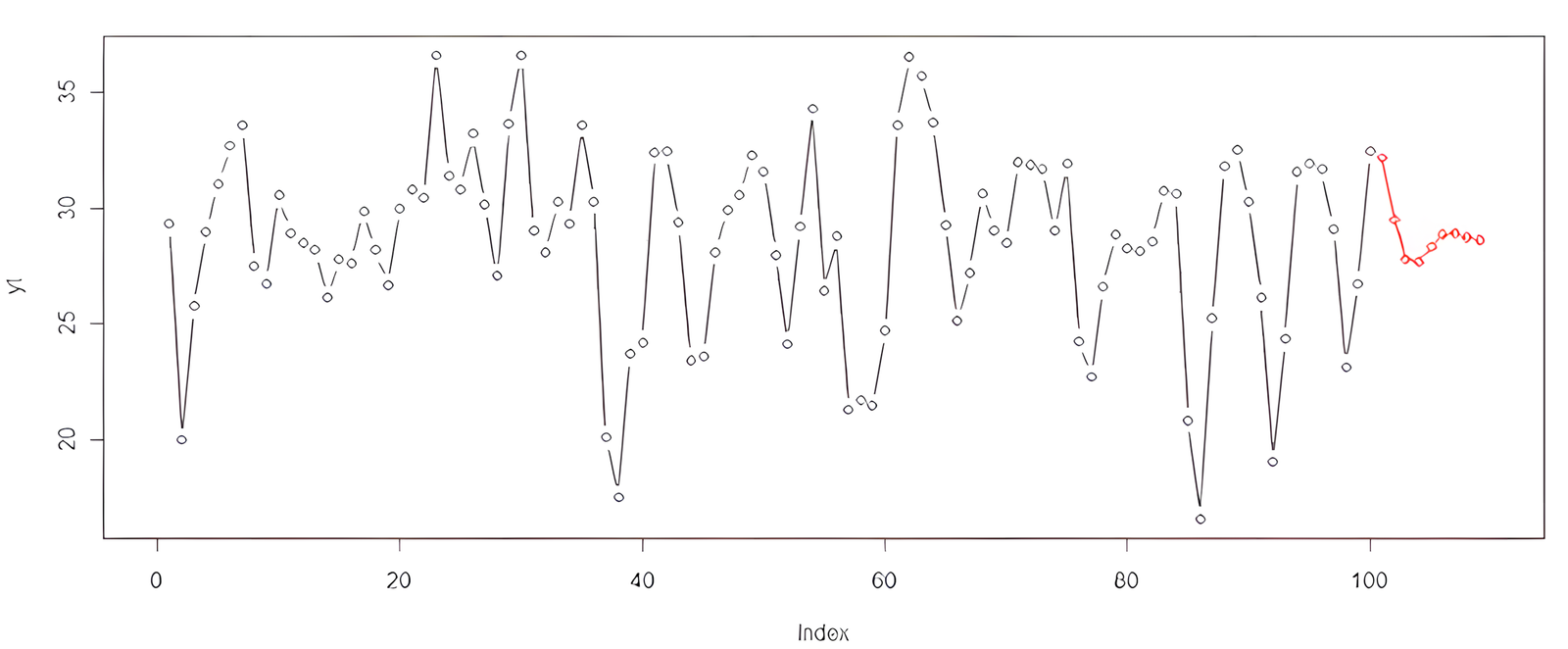
Vykreslenie pôvodného a predikovaného radu do jedného grafu:
plot(yt, type = "b", xlim = c(0, 110)) lines(prog$pred, type = "b", col = "red")
Výsledný graf zobrazí historické hodnoty (čierne body/spojnice) a predikované hodnoty (červená čiara) pre nasledujúcich 9 období.
Predikované hodnoty modelu ARIMA
Na základe výstupu z funkcie predict() boli vypočítané nasledujúce predikované hodnoty pre najbližších 9 časových období:
32.15551 29.53138 27.78701 27.66211 28.31450 28.83130 28.92144 28.76592 28.61708
Tieto hodnoty predstavujú očakávaný vývoj časového radu podľa odhadnutého AR(2) modelu. Môžu slúžiť ako podklad pre prognózovanie alebo rozhodovanie v ekonomických a finančných aplikáciách.
