Exponenciálne vyrovnávanie
Metóda exponenciálneho vyrovnávania je najviac používanou prognostickou metódou pre jej výpočtovú jednoduchosť a predovšetkým pre schopnosť rýchleho reagovania na posledné zmeny hodnôt časového radu. Metodika zohľadňuje minulý vývoj sledovanej veličiny pomocou jej vážených priemerov.
Definujeme exponenciálne vyrovnávanie v čase t pomocou nasledovného vzorca:
Kde:
- St – exponenciálny priemer v čase t
- α – vyrovnávajúca konštanta z intervalu <0,1>;
- ß = 1 – α – doplnková váha
- N – dĺžka časového radu
- k – vek pozorovaní (poradie v minulosti)
Ak je časový rad dostatočne dlhý, člen ßⁿS₀ z posledného výrazu možno vynechať. Potom vzorec predstavuje vážený súčet všetkých členov časového radu s exponenciálne klesajúcimi váhami:
Voľba vyrovnávajúcej konštanty
Voľbou vyrovnávacej konštanty α je určovaná rýchlosť prispôsobovania ďalšej predpovede k aktuálnej chybe predpovede. Ak je α vysoké, nová predpoveď silno reaguje na posledné pozorovanie. Naopak, ak je α blízko nuly, nové hodnoty sa viac spoliehajú na predchádzajúci trend.
Pri požiadavke na stabilitu modelu volíme nižšie hodnoty α. Ak požadujeme rýchlu reakciu na zmeny, volíme α vyššie. V literatúre sa často odporúča, aby α nepresahovala hodnotu 0,3.
Typy vyrovnávania podľa trendu
- Bez sezónnosti:
- Konštantný trend – Brownovo jednoduché exponenciálne vyrovnávanie
- Lineárny trend – Brownovo dvojité exponenciálne vyrovnávanie, Holtovo vyrovnávanie (2 konštanty)
- Kvadratický trend – Trojité exponenciálne vyrovnávanie
- So sezónnou zložkou:
- Holt-Wintersovo exponenciálne vyrovnávanie
Holt-Wintersov model
Pri použití Holt-Wintersovho exponenciálneho vyrovnávania sa predpokladá, že v čase t = 1, 2, 3, …, T je možné časový rad rozdeliť na lokálne lineárne trendy s konštantnou alebo multiplikatívnou sezónnosťou.
Aditívny model:
Multiplikatívny model:
Kde:
- b₀ – parameter úrovne lineárneho modelu
- b₁ – parameter smernice (sklonu) trendu
- εₜ – náhodná zložka
- t – časová premenná
- Sₜ – sezónny index/priemer v čase t
Pre sezónne priemery musí platiť:
Pre sezónne indexy musí platiť:
Vyrovnávajúce rovnice (α, β, γ)
V Holt-Wintersovom modeli používame tri vyrovnávajúce konštanty:
- α – pre úroveň (hladinu)
- β – pre trend
- γ – pre sezónnosť
Aditívny model – vyrovnávacie rovnice
Prognózovanie (aditívny model):
Multiplikatívny model – vyrovnávacie rovnice
Prognózovanie (multiplikatívny model):
Exponenciálne vyrovnávanie v R – nesezónne dáta
Najznámejšia funkcia v R pre exponenciálne vyrovnávanie je HoltWinters(), ktorá dokáže pracovať so sezónnymi aj nesezónnymi dátami. Je súčasťou základného R, takže netreba inštalovať žiadne balíky.
HoltWinters(x, alpha = NULL, beta = NULL, gamma = NULL, seasonal = c("additive", "multiplicative"))
Parametre funkcie:
- x – dáta časového radu
- alpha, beta, gamma – vyrovnávajúce konštanty
- seasonal – spôsob sezónnosti („additive“ alebo „multiplicative“). Funguje iba ak
gamma ≠ FALSE
Príklad – nesezónne dáta
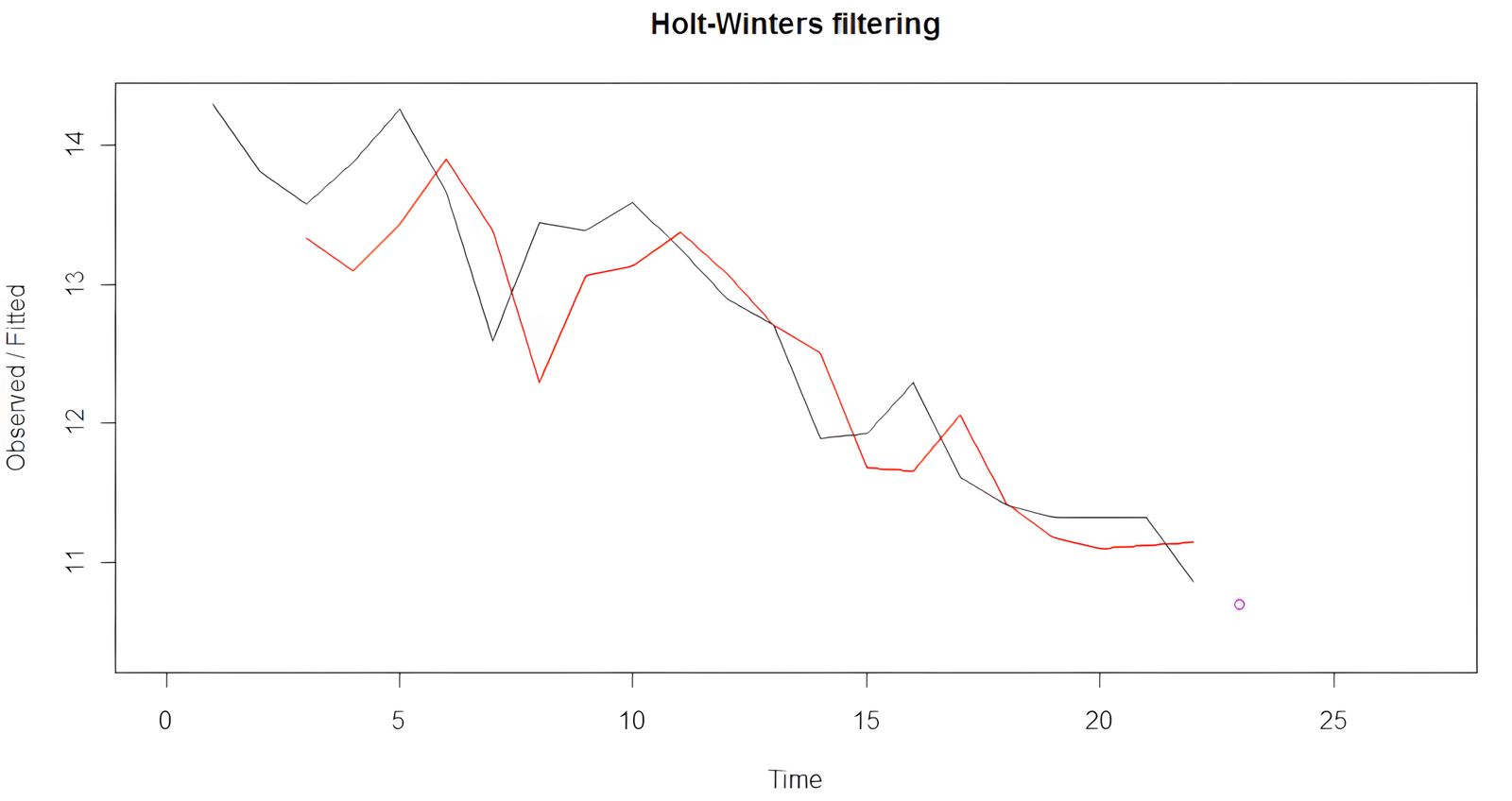
Ukážka použitia funkcie HoltWinters pre časový rad bez sezónnosti:
# načítanie dát
# Dáta použité v tomto príklade nájdete tu: Odkazy na použité a reálne dáta
# exponenciálne vyrovnávanie bez sezónnosti (gamma=FALSE)
yt.hw = HoltWinters(yt, gamma = FALSE)
# vykreslenie výstupu z funkcie HoltWinters
plot(yt.hw, xlim = c(0, length(yt) + 5), ylim = c(min(yt) - 0.5, max(yt)))
# výpočet prognózy na 1 krok dopredu
yt.hw.pred = predict(yt.hw, n.ahead = 1)
# vykreslenie predikcie
lines(yt.hw.pred, type = "p", col = "purple")
Exponenciálne vyrovnávanie v R – sezónne dáta
Aj pri dátach so sezónnosťou môžeme použiť funkciu HoltWinters(). Stačí zabezpečiť správny formát časového radu – najčastejšie mesačný (frekvencia 12).
Dáta použité v tomto príklade nájdete tu: Odkazy na použité a reálne dáta
# konverzia dát na časový rad (mesačné, od roku 1956)
yt <- ts(yt, start = 1956, freq = 12)
# exponenciálne vyrovnávanie so sezónnosťou
yt.hw = HoltWinters(yt)
# vykreslenie vyrovnaného radu
plot(yt.hw, xlim = c(1956, 1999))
# prognóza na 48 mesiacov dopredu
yt.hw.pred = predict(yt.hw, n.ahead = 48)
# vykreslenie predikcie do grafu
lines(yt.hw.pred, col = "purple")
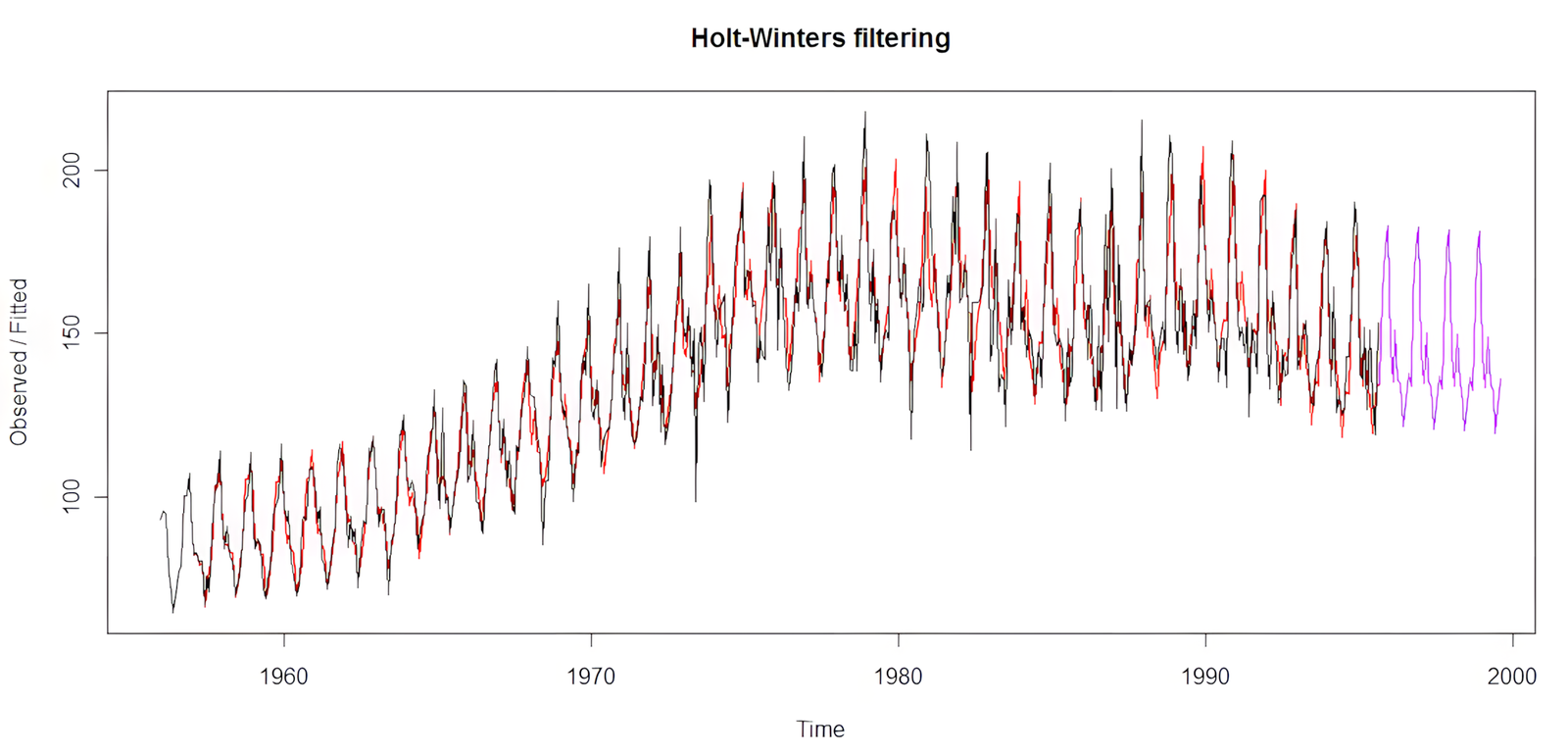
# odhad modelu HW (červená čiara v grafe)
c(yt.hw$fitted[,"xhat"])
Polívka, L.: DIPLOMOVÁ PRÁCA: Moderné prognostické metódy v modelovaní podnikových procesov. 2010
Zucchini, W., Nenadi, O.: Time Series Analysis with R – Part I [4.6. 2015]
