Užívateľský manuál

Táto stránka je aktuálne v procese tvorby. Ďakujeme za trpezlivosť!

Vo výrobe

Kalmanova filtrácia

Kalmanova filtrácia je metóda používaná na odhad aktuálneho a budúceho stavu dynamického systému. Je založená na tzv. Kalmanovom filtri, ktorý dokáže eliminovať šum z pozorovaní a získať čo najpresnejší odhad stavu systému.

Najčastejšie sa využíva v oblastiach ako GPS navigácia, vojenské riadenie, robotika, ale aj ekonómia a analýza časových radov. Aby bolo možné Kalmanov filter použiť, musí byť systém popísaný lineárnou stavovou formou.

Matematická formulácia

Stavová rovnica:

xt = A·xt-1 + B·ut-1 + wt-1
  • xt – stavový vektor
  • A – prechodová matica
  • B – matica parametrov exogénnych premenných
  • ut – vektor exogénnych premenných
  • wt – procesný šum, s kovarianciou Q

Rovnica pozorovaní:

yt = H·xt + vt
  • yt – pozorovanie
  • H – matica pozorovaní
  • vt – šum pozorovaní, nezávislý od wt, s kovarianciou R

Riešenie Kalmanovej filtrácie v R

Na riešenie Kalmanovej filtrácie v R môžeme využiť vstavanú funkciu StructTS(), ktorá umožňuje pracovať s rôznymi typmi štrukturálnych modelov. 

StructTS(x, type = c("level", "trend", "BSM"), 
         init = NULL, fixed = NULL, 
         optim.control = NULL)

Parametre:

  • x – časový rad (môže obsahovať chýbajúce hodnoty)
  • type – typ modelu: napr. "BSM" – základný štrukturálny model
  • init – počiatočné hodnoty rozptylu
  • fixed – voliteľný vektor pevných parametrov

Príklad na Kalmanovu filtráciu

V tomto príklade použijeme štvrťročné dáta z Českého štatistického úradu – konkrétne ide o počet osôb, ktoré strávili viac ako 4 noci v hoteloch v Českej republike.

Z dát vytvoríme časový rad s frekvenciou 4 (štvrťročne), so začiatkom v roku 2003, a vykreslíme ho do grafu. 

my_cv_data <- c(1446.10, 1940.17, 5576.95, 978.36,
               1410.89, 1500.21, 5068.24, 953.86,
               1338.31, 2036.41, 5005.75, 1052.94,
               1488.87, 1938.82, 5130.36, 1347.81,
               1516.84, 1922.73, 5792.79, 1220.65,
               1431.42, 1754.18, 5648.29, 1355.09)

ts_freq <- 4
ts_start <- 2003
mcdata_ts <- ts(my_cv_data, start = ts_start, frequency = ts_freq)
plot(mcdata_ts, lty = "dotted")

Pre vizualizáciu sezónnych zmien v čase načítame knižnicu forecast a použijeme funkciu seasonplot(): 

library(forecast)
seasonplot(mcdata_ts)

Tento graf umožňuje porovnať hodnoty rovnakých štvrťrokov naprieč rokmi, čo môže odhaliť sezónne vzory alebo odchýlky.

Predikcia Kalmanovou filtráciou

Po vytvorení modelu Kalmanovej filtrácie pomocou StructTS() môžeme pristúpiť k predikcii na nasledujúce obdobia. V tomto prípade predikujeme 4 štvrťroky dopredu: 

kts <- StructTS(mcdata_ts, type = "BSM")
prog_kts <- predict(kts, 4)

Pre vizualizáciu reálnych, odhadnutých aj predikovaných dát použijeme vlastnú funkciu plot_kalman(), ktorá ako parametre prijíma originálne dáta, model, predikciu a informácie o časovej osi: 

plot_kalman <- function(data_ts, kts, prog_kts, t.start, t.freq) {
  prog_kts <- prog_kts$pred
  kts_s <- kts$fitted[,1] + kts$fitted[,2] + kts$fitted[,3]
  min_v <- min(data_ts, prog_kts, kts_s)
  max_v <- max(data_ts, prog_kts, kts_s)
  kts_w_prog <- ts(c(kts_s, prog_kts), start = t.start, freq = t.freq)
  
  plot(data_ts, xlim = attr(kts_w_prog, "tsp")[1:2],
       ylim = c(min_v, max_v), lty = "dotted")
  lines(kts_w_prog, col = "red")     # Predikcia
  lines(kts_s, col = "blue")         # Kalman filter
}

Funkciu spustíme nasledovne: 

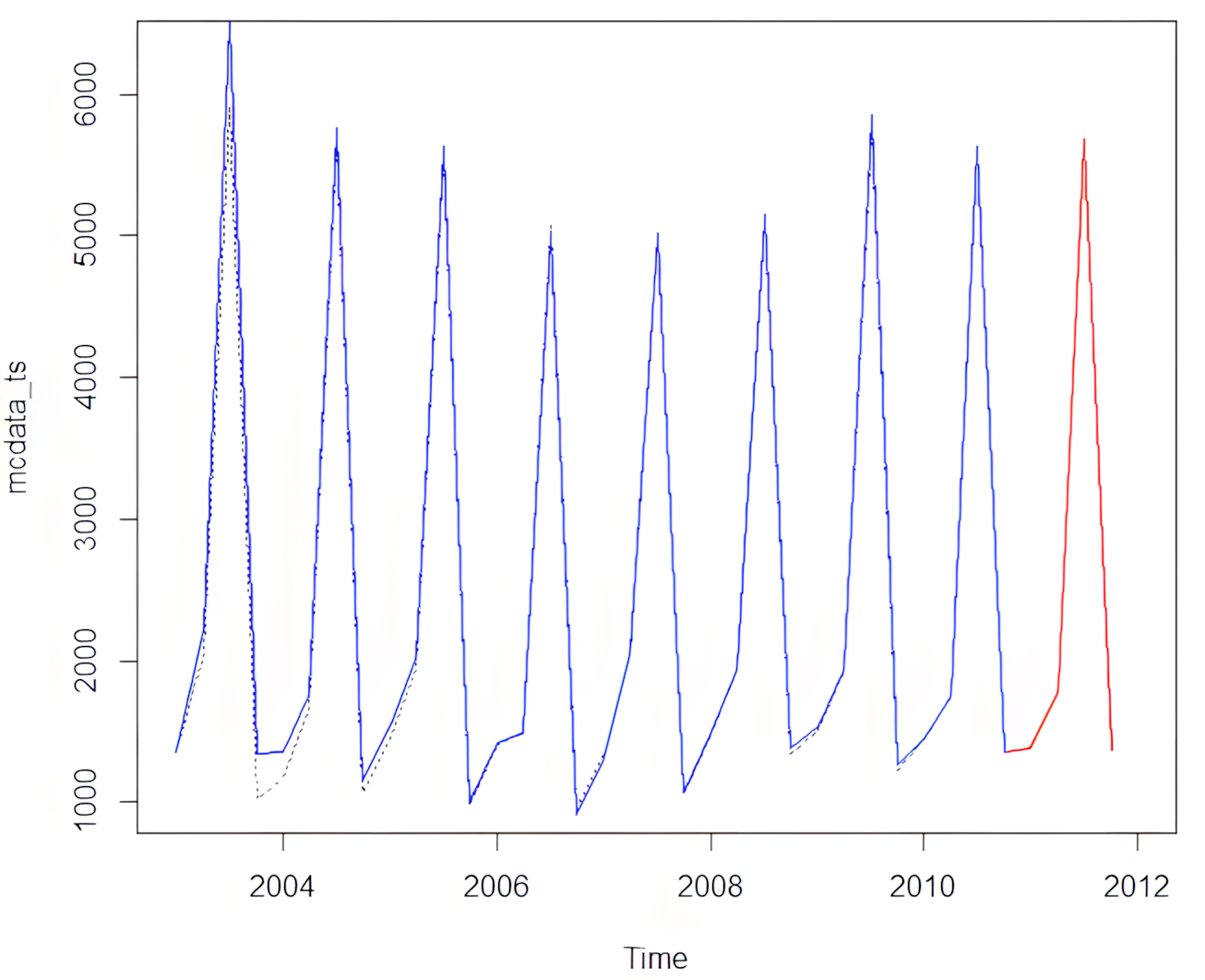
plot_kalman(mcdata_ts, kts, prog_kts, ts_start, ts_freq)

Výsledný graf zobrazí:

  • Reálne dáta (čiarkovaná čiara)
  • Kalmanom odhadnuté hodnoty (modrá čiara)
  • Predikcie na ďalšie 4 kvartály (červená čiara)

Výpočet RMSE pre Kalmanovu filtráciu

Na overenie kvality odhadu Kalmanovým filtrom môžeme použiť odmocnenú priemernú štvorcovú chybu (RMSE – Root Mean Squared Error). RMSE vypočítame ako odmocninu z priemeru druhých mocnín rozdielov medzi odhadovanými hodnotami kts$fitted a pôvodnými dátami mcdata_ts. 

RMSE_kalman <- sqrt(sum((rowSums(kts$fitted) - mcdata_ts)^2) / length(mcdata_ts))
RMSE_kalman
# [1] 136.4347

Nižšia hodnota RMSE znamená lepší model – teda presnejšie odhady pôvodných dát pomocou Kalmanovej filtrácie.

Zdroj: Považanec, P.: Diplomová práca: Optimalizácia softvérového riešenia prognózovania časových radov ekonomických dát. 2010

Zhrnutie z exponenciálneho vyrovnávania
Návrat hore