Užívateľský manuál

Táto stránka je aktuálne v procese tvorby. Ďakujeme za trpezlivosť!

Vo výrobe

Spektrálna analýza

Prognózovanie s využitím spektrálnej analýzy predstavuje prístup, ktorý využíva transformáciu časového radu do frekvenčnej domény. Jej cieľom je identifikovať dominantné cykly, sezónne vplyvy a šumové komponenty v dátach. Spektrálna analýza môže byť veľmi užitočná najmä pri dekompozícii zložitých signálov.

V literatúre je dobre zdokumentovaná schopnosť spektrálnej analýzy odhaliť primárne cykly, dlhodobé trendy či sezónnosť. Avšak jej samotné využitie na prognózovanie býva často doplnené o ďalšie metódy.

V praxi sa spektrálna analýza kombinuje s Jednoduchou metódou najmenších štvorcov (JMNŠ), pričom sa najprv pomocou periodogramu identifikujú významné frekvenčné zložky. Časový rad je potom reprezentovaný ako lineárna kombinácia sínusových a kosínusových funkcií.

Po kvantifikácii modelu pomocou JMNŠ sa vykoná verifikácia modelu. Ak sú výsledky pozitívne, model je možné použiť na výpočet prognóz pre budúce hodnoty časovej premennej.

Tento prístup ukazuje, že časová a frekvenčná doména sa pri analýze časových radov nevylučujú, ale dopĺňajú, čím rozširujú možnosti modelovania a predikcie.

Fourierova reprezentácia časového radu

Podstatou spektrálnej analýzy je vyjadrenie časového radu ako lineárnej kombinácie periodických funkcií rôznych frekvencií a amplitúd. Hoci rad nemusí byť explicitne periodický, jeho skryté cyklické zložky môžu byť odhalené práve touto technikou.

Na transformáciu sa bežne používajú sínusové a kosínusové funkcie. Výsledný vzťah je známy ako Fourierova reprezentácia časového radu a vyzerá nasledovne:

Fourierova reprezentácia
  • A₀ – konštantná zložka
  • m – počet harmonických (m = N/2 pre párne N, m = (N−1)/2 pre nepárne N)
  • Aj, Bj – amplitúdy jednotlivých cyklov
  • fj – Fourierove frekvencie, napr. f = {1/N, 2/N, …, k/N}

Frekvencie fj sa udávajú v cykloch za jednotku času, pričom ich radiánový ekvivalent je uhlová frekvencia ωj = 2πfj.

Fourierova reprezentácia je univerzálna a možno ju aplikovať aj na rad bez zjavnej periodicity. Umožňuje rozklad signálu na základné harmonické zložky, čo je veľmi užitočné pri detekcii sezónnosti alebo cyklických vzorcov.

Príklad použitia spektrálnej analýzy a periodogramu

V tomto príklade si ukážeme, ako vytvoriť syntetický časový rad zložený z troch harmonických zložiek s rôznymi frekvenciami a amplitúdami.

Vstupné vzorce pre jednotlivé zložky:

  • Yₜ₁ = 2 · cos(2πt · 6/100) + 3 · sin(2πt · 6/100)
  • Yₜ₂ = 4 · cos(2πt · 10/100) + 5 · sin(2πt · 10/100)
  • Yₜ₃ = 6 · cos(2πt · 40/100) + 7 · sin(2πt · 40/100)

Výsledný časový rad je súčtom týchto troch zložiek:
Yₜ = Yₜ₁ + Yₜ₂ + Yₜ₃

Implementácia v R:

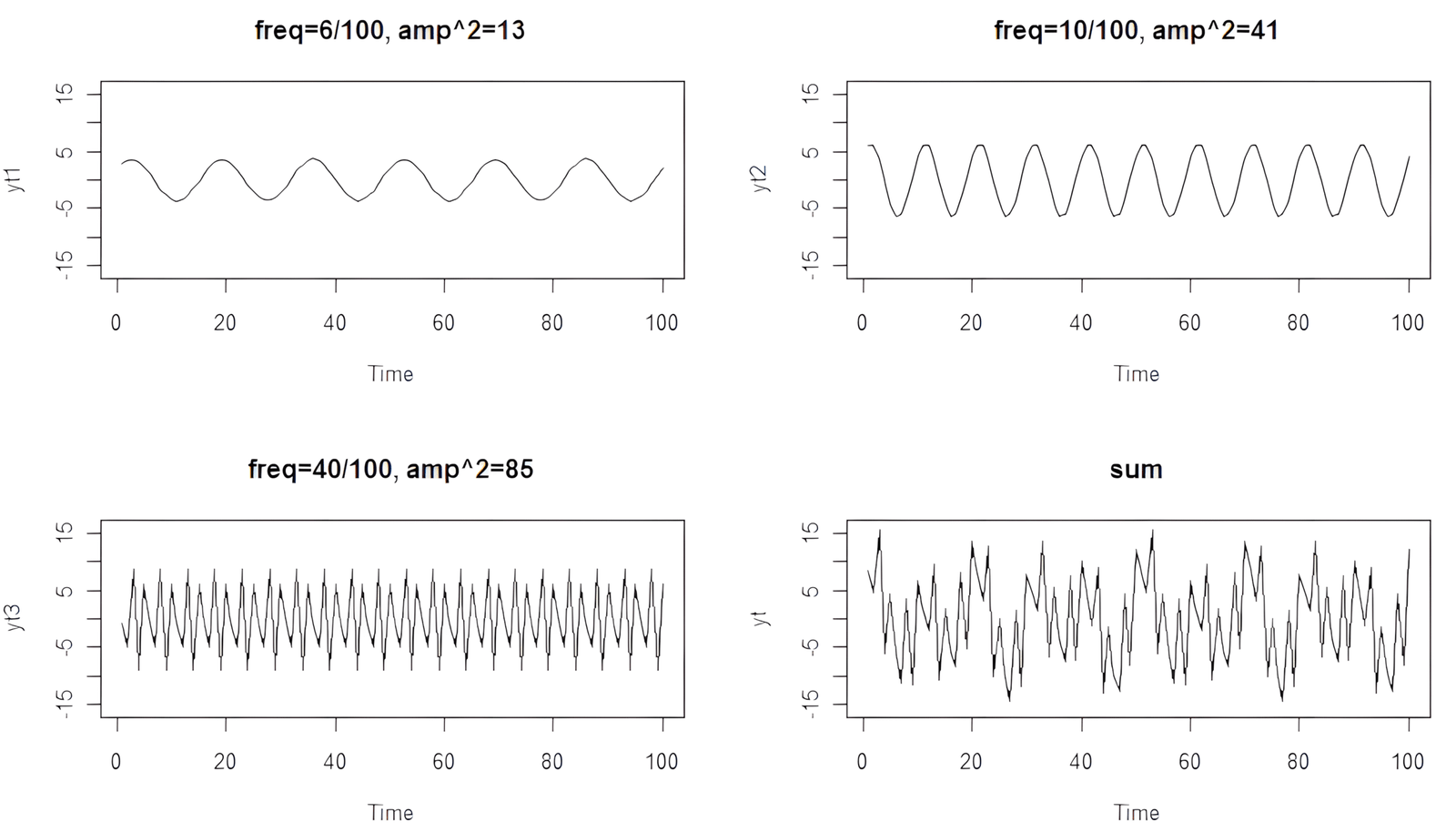
# definujeme rozsah t
t = 1:100

# jednotlivé harmonické zložky
yt1 = 2*cos(2*pi*t*6/100) + 3*sin(2*pi*t*6/100)
yt2 = 4*cos(2*pi*t*10/100) + 5*sin(2*pi*t*10/100)
yt3 = 6*cos(2*pi*t*40/100) + 7*sin(2*pi*t*40/100)

# výsledný časový rad
yt = yt1 + yt2 + yt3

# vykreslenie zložiek a ich súčtu
par(mfrow=c(2,2))
plot.ts(yt1, ylim=c(-16,16), main="freq=6/100, amp²=13")
plot.ts(yt2, ylim=c(-16,16), main="freq=10/100, amp²=41")
plot.ts(yt3, ylim=c(-16,16), main="freq=40/100, amp²=85")
plot.ts(yt, ylim=c(-16,16), main="Súčet harmonických zložiek")

Tento syntetický príklad slúži ako skvelá ukážka toho, ako periodogram a spektrálna analýza môžu identifikovať frekvenčné zložky v komplexnom signále.

Výpočet a vizualizácia periodogramu pomocou FFT:

# výpočet periodogramu cez FFT
P = abs(2 * fft(yt) / 100)^2

# frekvenčná os pre zobrazenie (0 až 0.5)
f = 0:50 / 100

# vykreslenie periodogramu
plot(f, P[1:51], type = "o", xlab = "frequency", ylab = "periodogram")

Periodogram nám umožňuje vizuálne identifikovať dominantné frekvenčné zložky v časovom rade. Vrcholy v grafe zodpovedajú frekvenciám, ktoré majú v date najväčší podiel.

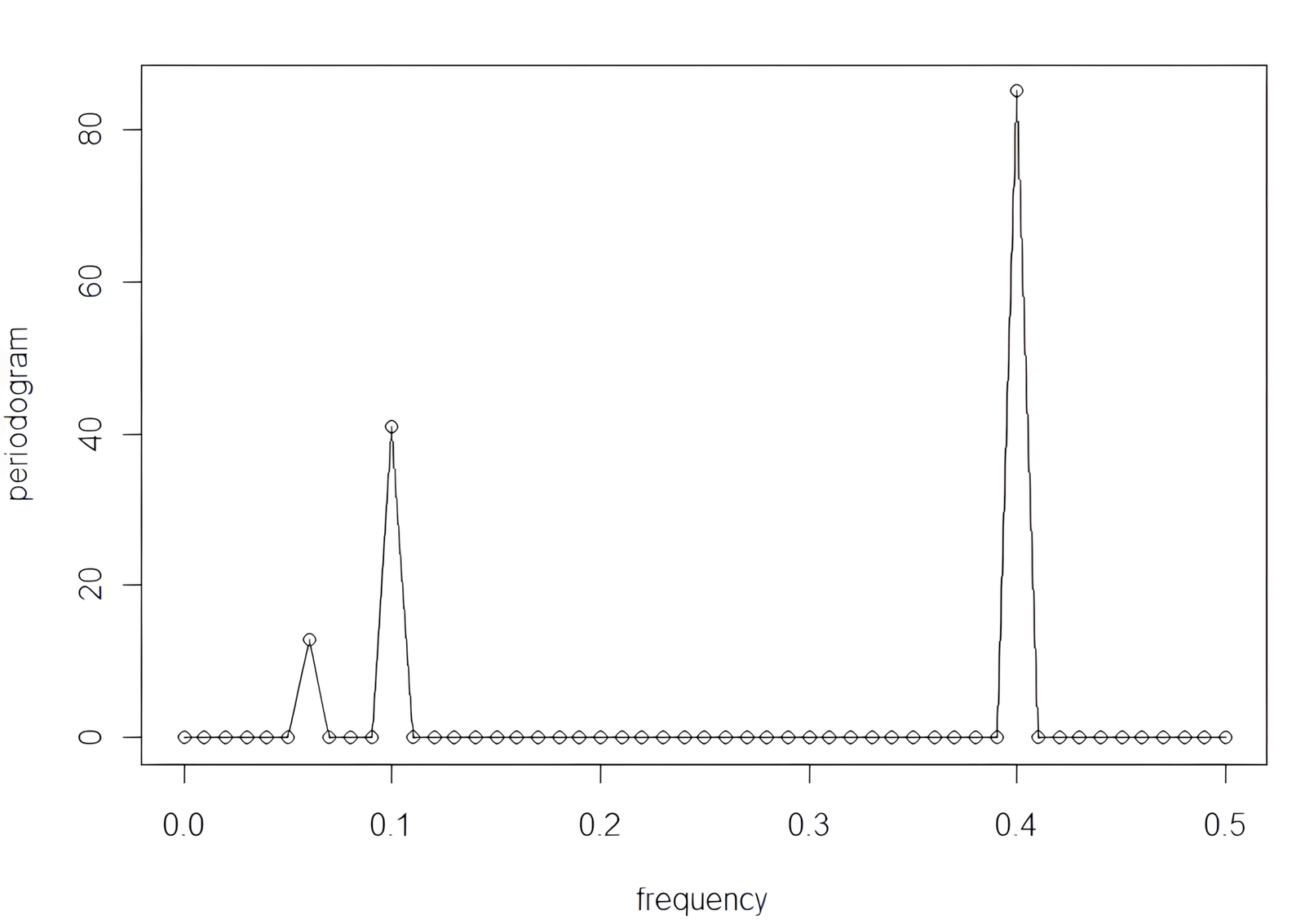
Tento periodogram jednoznačne určuje zložky Yt1, Yt2 a Yt3. Ako môžme vidieť, jednotlivé výšky sú:

  • P(6/100) = 13
  • P(10/100) = 41
  • P(40/100) = 85

Keby sme považovali dáta Yt za farbu, vytvorenú z primárnych farieb Yt1, Yt2 a Yt3 rôznej intenzity (amplitúdy), tak potom môžeme chápať periodogram ako dekompozíciu farby Yt na jej primárne zložky – teda spektrum. Preto termín spektrálna analýza.

Zdroje:
Jurčo, M.: DIPLOMOVÁ PRÁCA: Modelovanie sezónnosti v ekonomických procesoch s využitím aplikácie Open Source. 2010
Shumway, R., Stoffer D.: Time Series Analysis and Its Applications With R Examples. New York: Springer Science + Business Media, 2011. ISBN 978-1-4419-7864-6

Zhrnutie z exponenciálneho vyrovnávania
Návrat hore