Užívateľský manuál

SV regresia

SV regresia (Support Vector Regression – SVR) je technika založená na princípoch strojového učenia, ktorá rozširuje základný koncept Support Vector Machines (SVM) pre regresné úlohy. Na rozdiel od tradičných lineárnych regresií, SVR nepredpokladá lineárnu závislosť medzi premennými a je schopná pracovať aj s nelineárnymi vzťahmi pomocou kernelových funkcií.

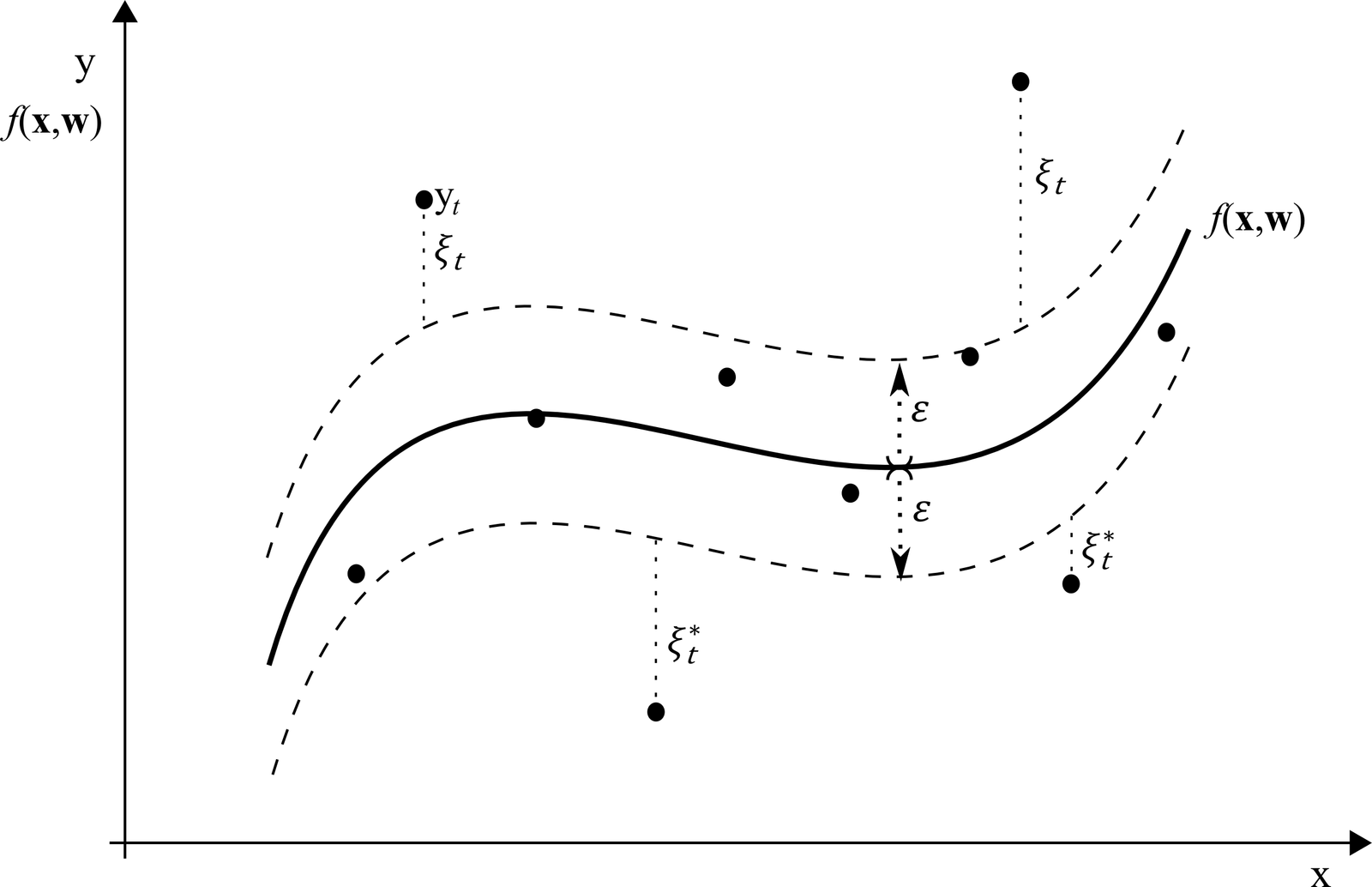
SVR sa snaží nájsť funkciu, ktorá má maximálnu presnosť, pričom toleruje malú chybu ε v predikcii. Pri optimalizácii sa hľadajú len tie pozorovania, ktoré prekračujú túto tolerančnú hranicu – tzv. „support vectors“ – čo robí SVR robustnou voči šumu a odľahlým hodnotám.

Táto metóda je vhodná najmä pri komplexnejších dátach, kde tradičné metódy zlyhávajú kvôli nelinearite alebo veľkej dimenzionalite dát. V oblasti ekonomických predikcií či analýz časových radov sa SV regresia ukazuje ako silný nástroj.

SVM v R

V R je metóda Support Vector Machines implementovaná vo viacerých knižniciach ako kernlab, klaR, svmpath či e1071. Najčastejšie sa využíva knižnica e1071, ktorá je postavená na populárnej knižnici LIBSVM.

Načítanie knižnice:

library(e1071)

Trénovanie modelu pomocou funkcie svm():

svm(x, y = NULL, scale = TRUE, type = NULL,
    kernel = "radial", degree = 3, gamma = if (is.vector(x)) 1 else 1 / ncol(x),
    coef0 = 0, cost = 1, nu = 0.5, class.weights = NULL, cachesize = 40,
    tolerance = 0.001, epsilon = 0.1, shrinking = TRUE, cross = 0,
    probability = FALSE, fitted = TRUE, ..., subset,
    na.action = na.omit)

Najdôležitejšie parametre:

• formula – symbolický zápis modelu
• x – vstupné premenné
• y – cieľová premenná (hodnoty)
• data – dátový rámec s premennými
• type – typ SVM metódy:
  • eps-regression – základná SVR regresia
  • nu-regression – alternatívna SVR
• kernel – typ kernel funkcie:
  • linear, polynomial, radial, sigmoid
• cost – penalizačný parameter (C)
• epsilon – šírka ε-pásma (tolerancia v stratovej funkcii)

Optimalizácia parametrov:
Na ladenie hyperparametrov podľa MSE slúži funkcia tune().

Predikcia nových hodnôt:
Po vytvorení modelu sa predikcia realizuje cez funkciu predict.svm().

Príklad použitia SVR v R

Pre ilustráciu predpokladajme, že hodnoty časového radu y sú závislé na jeho predchádzajúcich dvoch hodnotách x1 a x2. Dáta sú načítané ako data.frame s názvom dataset.

Tréning modelu:

model = svm(y ~ x1 + x2, data = dataset,
            type = "eps-regression",
            kernel = "linear",
            cost = 1,
            epsilon = 0.01)

Predikcia a výpočet RMSE:

predictions = predict(model, dataset)
rmse = sqrt(mean((dataset$y - predictions)^2))

Vizualizácia reálnych vs. predikovaných hodnôt:

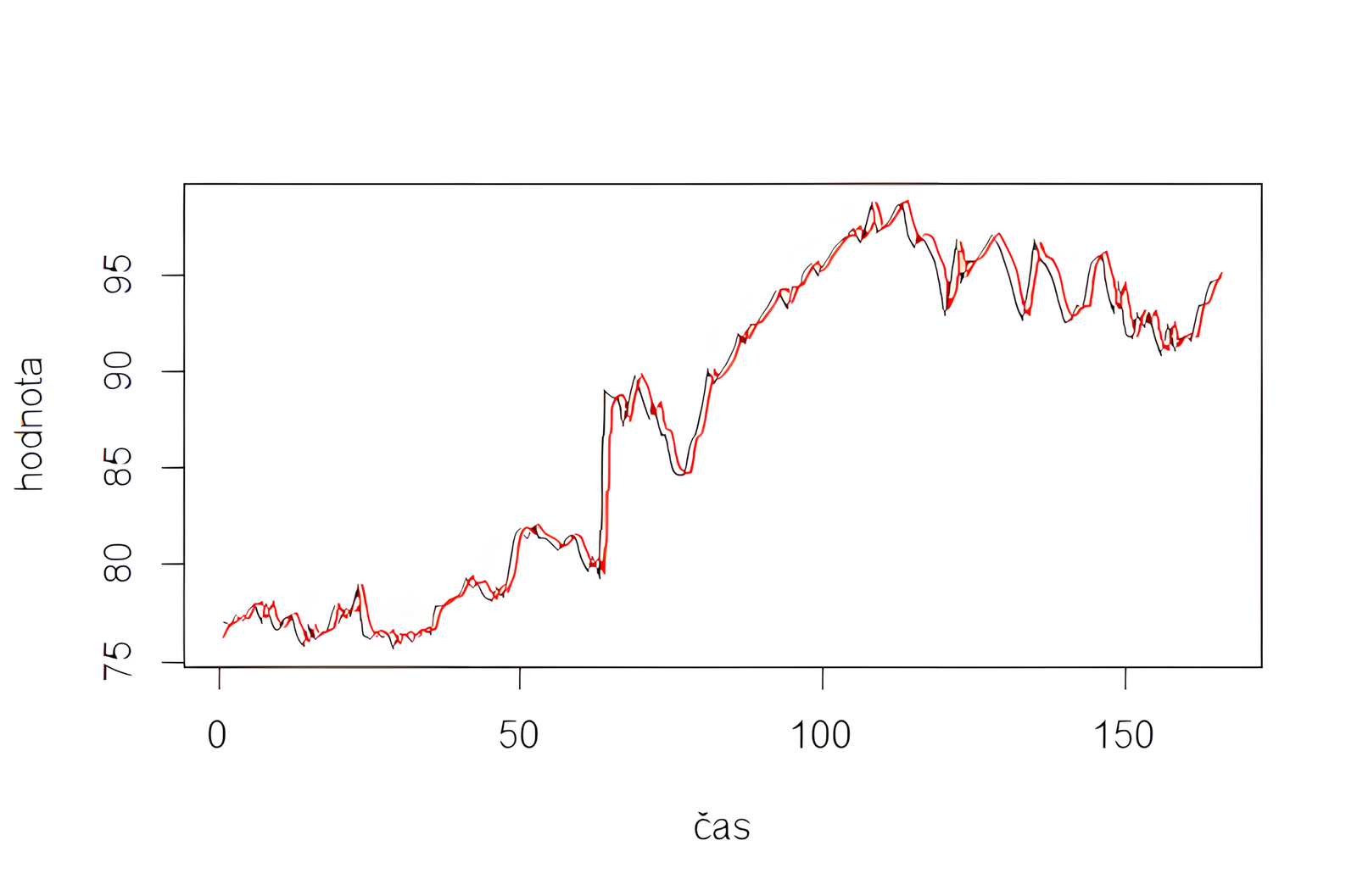
plot(dataset$y, type = "l", main = "SVR Predikcia vs. Skutočné dáta", ylab = "y", xlab = "Index")
lines(predictions, col = "red")

Červená čiara zobrazuje predikované hodnoty z modelu, ktoré by sa mali približovať k pôvodnému priebehu časového radu.

Optimalizácia parametrov SVR modelu

Najdôležitejšími parametrami SVR modelu sú epsilon a cost, ako aj výber kernel funkcie. Tieto parametre možno optimalizovať pomocou preddefinovanej funkcie tune() z knižnice e1071:

tunedModel = tune(svm, y ~ x1 + x2, data = dataset,
                  ranges = list(epsilon = seq(0, 1, 0.1),
                                cost = 2^(2:9)))
print(tunedModel)
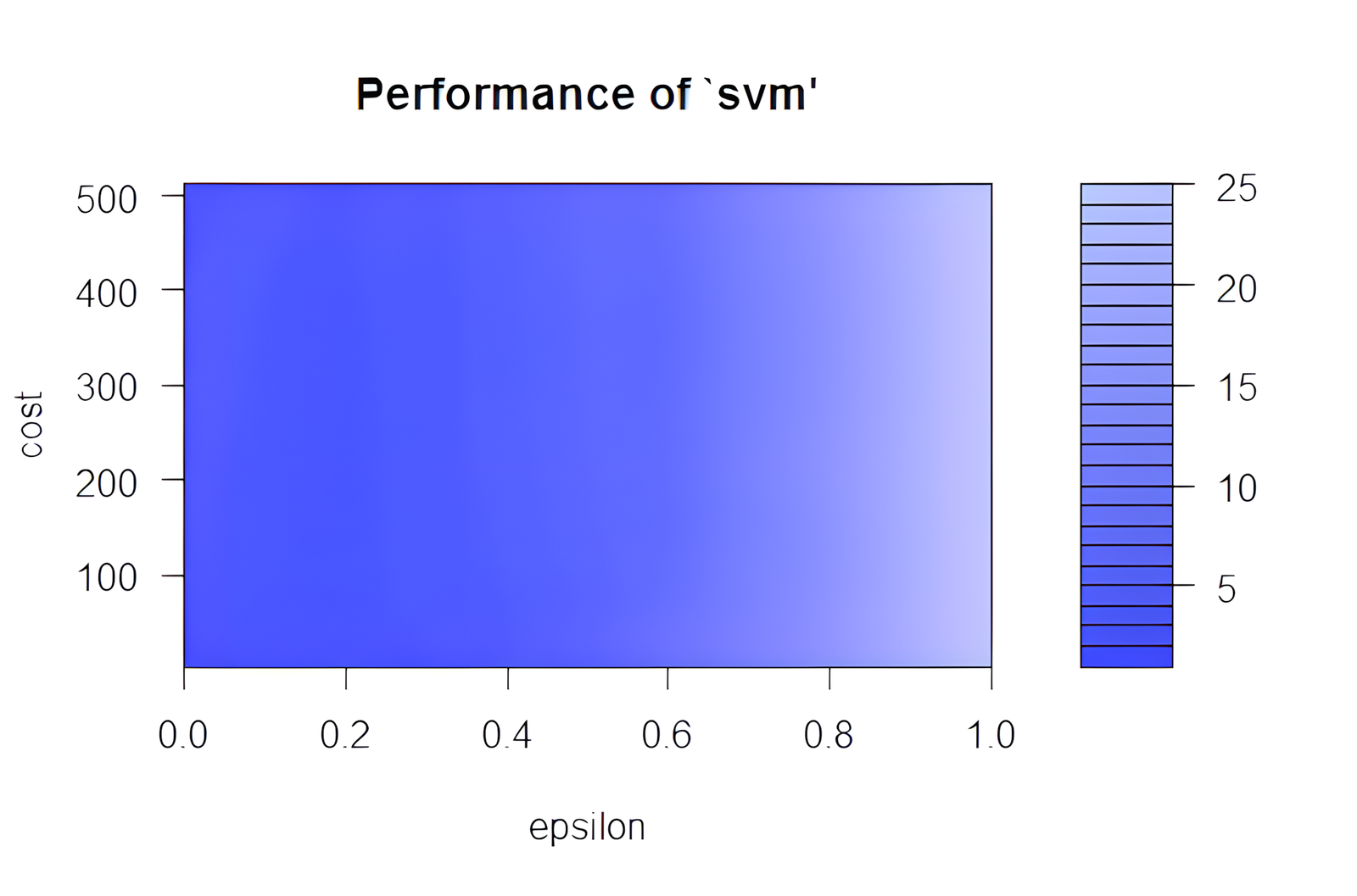
plot(tunedModel)

Výstup tunedModel obsahuje informácie o najlepšej kombinácii parametrov na základe MSE. Často je užitočné spustiť funkciu viackrát s menším krokom v okolí najlepšej oblasti z predchádzajúceho výpočtu.

Vlastná optimalizácia parametrov

Pre väčšiu flexibilitu môžeme optimalizovať parametre ručne cez cykly, kde si volíme hodnoty cost a gamma pre radial kernel:

trainset = dataset[1:100,]
testset = dataset[101:166,]
costs = 2^seq(from = -3, to = 5, by = 2)
gammas = 2^seq(from = -4, to = 4, by = 1)
rmses = matrix(nrow = length(costs), ncol = length(gammas))

for(i in 1:length(gammas)) {
  for(j in 1:length(costs)) {
    model = svm(y ~ x1 + x2, data = trainset,
                type = "eps-regression",
                kernel = "radial",
                cost = costs[j],
                gamma = gammas[i])
    predictions = predict(model, testset)
    rmses[j, i] = sqrt(mean((testset$y - predictions)^2))
  }
}

Do tabuľky rmses sa ukladajú hodnoty RMSE pre každú kombináciu cost a gamma. Túto tabuľku je možné ďalej vizualizovať alebo analyzovať ako náhradu za graf z funkcie tune.

Zdroj: Kecman, V. (2001); Slavík, M. (2015); e1071 package documentation